Аннотация: Статья посвящена вопросу применения метода имитационного моделирования при исследовании работы отделения банка как системы массового обслуживания. Сложность и непредсказуемое поведение системы может привести к тому, что результаты аналитического моделирования могут серьезно отличаться от реального поведения системы не только количественно, но и качественно, поэтому при изучении поведения реальных систем необходимо делать серьезные упрощения. Если вопросы, ответ на которые должна дать модель, относятся не к выяснению фундаментальных законов и причин, определяющих динамику реальной системы, а к практическому анализу ее поведения, то оправданным является применение имитационного моделирования.

Для изучения особенностей функционирования и оценки показателей эффективности работы отделения банка по обслуживанию физических лиц представлена имитационная модель системы массового обслуживания, входной поток заявок которой имеет показательное распределение, а время обслуживания клиентов подчинено нормальному закону распределения. Компьютерный эксперимент проведен в среде моделирования SimEvents системы MATLAB Simulink и средствами табличного процессора MS Excel. Приведены результаты имитационного моделирования процесса функционирования отделения банка и проведен анализ показателей эффективности его работы. Полученные результаты подтверждают универсальность и эффективность дискретно-событийного подхода к имитационному моделированию для диагностики работы и оптимизации структуры систем массового обслуживания. Применение современных средств визуально-ориентированного программирования позволяет использовать возможности виртуальных средств регистрации и визуализации результатов.

Annotation: The article is devoted to the application of the simulation method for the study of the work of the bank branch as a queuing system. Complexity and unpredictable behavior of the system can lead to the fact that the results of analytical modeling can seriously differ from the real behavior of the system not only quantitatively, but also qualitatively, therefore, when studying the behavior of real systems, serious simplifications must be made. If the questions the model should answer are not to clarify the fundamental laws and the causes that determine the dynamics of a real system, but to a practical analysis of its behavior, then the use of simulation modeling is justified.

To study the features of the functioning and evaluation of the performance indicators of the bank's department for servicing individuals, the simulation model of the queuing system is presented, the input stream of applications of which has an indicative distribution, and the customer service time is subject to the normal distribution law. Computer implementation of the model is in the environment of SimEvents of MATLAB+Simulink and implemented by MS Excel spreadsheet processor. The results of simulation modeling of the functioning of the bank branch are given and the analysis of performance indicators of its work is carried out. The obtained results confirm the versatility and efficiency of discrete-event approach to simulation modeling of queueing systems. The use of modern means of visual-oriented programming makes it possible to use the capabilities of virtual means of registration and visualization of results.

Введение

Управление в современном мире становится все более сложным, поскольку организационные структуры постоянно усложняются. Эта сложность объясняется характером взаимоотношений между различными элементами экономических систем и физическим системами, с которыми они взаимодействуют. Одним из наиболее важных и полезных инструментом анализа структуры сложных процессов и систем является имитационное моделирование [1, 2, 5, 6, 8]. На сегодняшний день имеется большое количество программных продуктов, направленных как на решение узкого круга задач, так и более универсальные, предназначенные для моделирования различных явлений и процессов [10, 12]. Все это предоставляет широкие возможности для эффективной работы специалистов различных профилей [17, 18].

При решении задач оптимизации управления, в том числе в сфере банковской деятельности, приходится иметь дело с системами массового обслуживания (СМО), предназначенными для выполнения некоторого потока требований, которые поступают на вход системы в случайные моменты времени. Обслуживание этих заявок в общем случае длится случайное время. Именно случайный характер потока заявок и времени их обслуживания приводит к неравномерной загруженности СМО. При формализации задач обслуживания вполне естественно стремление построить СМО таким образом, чтобы установить разумный компромисс между показателями, связанными с обслуживанием заявок и полнотой использования возможностей системы. В связи с этим необходимо выбрать такой показатель эффективности СМО, который учитывает одновременно требования и возможности и тех, кого обслуживает, и тех, кто обслуживает [4, 19, 22]. В работе [3] в качестве показателя экономической эффективности выбран минимум затрат, связанных с обращением системы (затраты, связанные с эксплуатацией СМО и простоем каналов обслуживания) и обслуживания заявок (потери, связанные с пребыванием заявок в очереди и с уходом не обслуженных заявок). В работе [14] представлена комплексная статистическая имитационная модель СМО торгового предприятия, оптимизация которой заключается в определении такого числа каналов обслуживания, при котором число обслуженных заявок обеспечивает максимум функции чистой прибыли, учитывающей налоговые отчисления, размер заработной платы кассиров и стимулирующие надбавки персоналу, величину наценки на товары различных категорий и недополученную прибыль от различных категорий товаров.

Реальные системы массового обслуживания, как правило, состоят из большого числа элементов и имеют сложные внутренние связи. Использование аналитических моделей в таких случаях не позволяет получить достоверных результатов и зачастую для построения и изучения СМО переходят к имитационным моделям [4, 7].

Для проведения имитационного эксперимента существует достаточно широкий перечень специальных программных продуктов, среди которых можно выделить MATLAB Simulink, GPSS World, AnyLogic, Arena, iThink, PowerSim и другие [15, 16, 20, 21, 23]. Однако далеко не всегда имеется возможность установить эти программы. Выходом из данной ситуации может оказаться проведение имитационного эксперимента с помощью табличного процессора MS Excel. Такой подход позволяет получить неплохие результаты при моделировании систем массового обслуживания.

Задачей данной работы является построение имитационной модели деятельности отделения банка по обслуживанию физических лиц на основе дискретно-событийного подхода с помощью табличного процессора MS Excel.  Для оценки приемлемости полученных результатов моделирования проведем аналогичный эксперимент в среде MATLAB+Simulink. При этом отделение банка рассматривается как система массового обслуживания с s устройствами, каждое из которых может одновременно обслуживать только одно требование.

Постановка задачи моделирования

Программная модель системы массового обслуживания должна адекватно отражать поведение элементов системы в процессе ее функционирования, т.е. в их взаимодействии друг с другом и внешней средой, и в то же время не создавать трудностей при ее реализации.

В основе разработки программной реализации СМО используется принцип дискретно-событийного моделирования, который используется для построения моделей, отражающих развитие системы во времени, когда состояния переменных системы меняются мгновенно в конкретные моменты времени [13]. Состояние системы определяется как совокупность переменных, необходимых для ее описания на определенный момент времени в соответствии с задачей исследования. Например, при исследовании работы банка переменными состояния могут служить число занятых кассиров, число посетителей в банке, время прибытия каждого клиента в банк и др. В качестве критерия остановки прогона при имитационном моделировании могут выступать обработка определенного количества требований или достижение определенного времени моделирования. При моделировании СМО также следует учитывать влияние вида закона распределения входного потока заявок на статистические характеристики выходных параметров системы. Поэтому оптимизировать характеристики эффективности системы в целом невозможно без учета влияния вида закона распределения входного потока заявок [11].

Интервалы времени между поступлением требований являются независимыми случайными величинами со средним значением µ_A. Время обслуживания также является случайной некоррелированной с интервалами поступления требований величиной. Среднее значение времени обслуживания требований – µ_S.  В качестве входных параметров системы выберем количество каналов обслуживания s, среднее время поступления заявок µ_A, среднее время обработки требований µ_S, длину очереди l. В качестве выходных параметров системы будем рассматривать следующие показатели: коэффициент использования системы, среднее время ожидания заявки в очереди, среднее время пребывания заявки в системе, среднее по времени число требований в очереди, среднее по времени число требований в системе, относительная пропускная способность системы. При оценке эффективности работы СМО необходимо сопоставить доходы от выполнения заявок с потерями от простоя каналов обслуживания (с одной стороны будем иметь высокую пропускную способность, а с другой стороны – значительный простой каналов обслуживания) и выбрать компромиссное решение.

Пример имитационной модели работы отделения банка по обслуживанию физических лиц с помощью MS Excel.

Рассмотрим работу отделения банка по обслуживанию физических лиц с дисциплиной обслуживания – FIFO (First-In, First-Out) – очередь: требования обслуживаются по принципу «первым пришел – первым обслужен». Для исследования интенсивности входного потока заявок собрана статистическая информация. В течение каждого дня недели время поступления клиентов изменяется от 9:00 до 20:00 часов. Время между приходом двух клиентов является случайной величиной с показательным законом распределения (µ_A = 5 мин), а время обслуживания подчиняется нормальному закону распределения с математическим ожиданием µ_S = 6.5 мин и средним квадратическим отклонением 2 мин. В том случае, если в момент прихода нового клиента оператор занят, то клиент встает в очередь. При этом имеются места ожидания, число которых равно 10. Для работы по обслуживанию клиентов привлечены 2 оператора-кассира. Реализация процесса имитационного эксперимента средствами MS Excel представлена на рисунке 1.

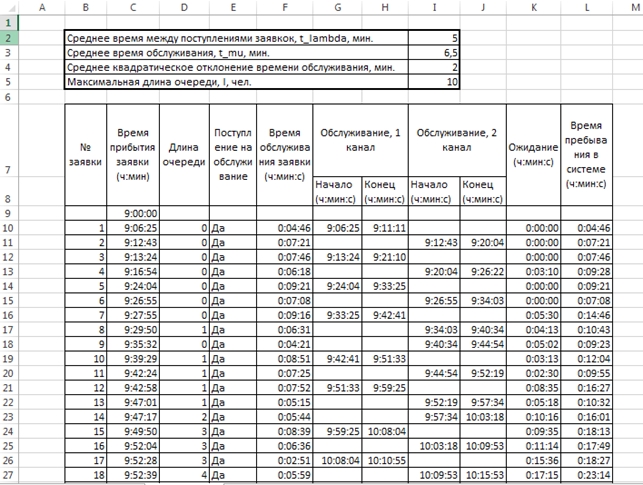
Рисунок 1. Моделирование работы отделения банка при наличии двух операторов-кассиров

 

По результатам проведения имитационного эксперимента работы отделения банка по обслуживанию физических лиц средствами MS Excel можно сделать следующие выводы:

– в течение одного рабочего дня в отделение приходит в среднем 127 клиентов, из которых обслуженными оказываются 126 человек, при этом на момент окончания моделирования 1 клиент находится на обслуживании, очереди нет. Таким образом, относительная пропускная способность рассматриваемой СМО составляет 99.2%;

– среднее время ожидания клиентом обслуживания составляет 2.67 минут;

– среднее число клиентов, находящихся в очереди составляет 0.54 человека;

– в течение рабочего дня оба оператора оказываются равномерно загруженными и обслуживают 62 и 64 клиента соответственно, при этом коэффициент использования системы составляет 62.05%.

Анализ показателей эффективности системы обслуживания клиентов свидетельствует о нормальной работе отделения банка по обслуживанию физических лиц при наличии двух операторов-кассиров.

Пример имитационной модели в среде MATLAB+Simulink

Для проведения имитационного эксперимента работы отделения банка в течение одного рабочего дня выбрана среда моделирования SimEvents пакета MATLAB+Simulink, имеющего большой набор различных блоков, которые обеспечивают различные воздействия с временными и функциональными зависимостями, а также блоки получателей информации [9].

При дискретно-событийном моделировании используется понятие сущностей (entities), которые могут перемещаться через сети очередей (queues), серверов (servers) и переключателей (switches), управляемых дискретными событиями, в процессе моделирования. Графические блоки SimEvents могут представлять компонент, который обрабатывает сущности, но сами сущности не имеют графического представления. Ключевые процессы моделирования состоят их следующих основных блоков: генерации сущностей (блок Time-BasedEntityGenerator), хранения сущностей в очереди (блок FIFO Queue), обслуживания сущностей (блок SingleServer) и отображения информации о ходе моделирования (блоки SignalScope или Display). Для каждого блока необходимо установить параметры, которые соответствуют требованиям моделируемой системы.

Установим время моделирования 660 мин., что соответствует времени работы отделения с 9:00 до 20:00. Схема полученной модели и результаты моделирования представлены на рисунке 2.

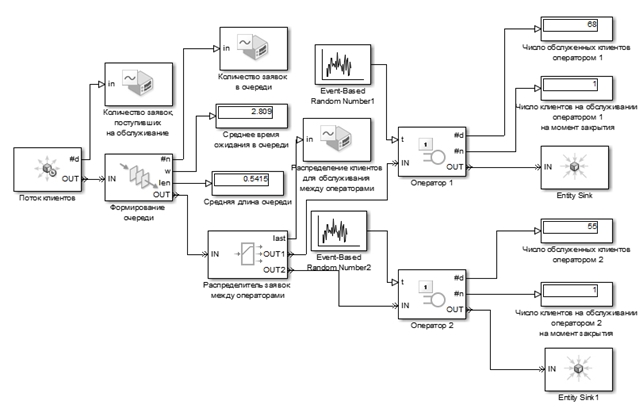
Рисунок 2. Схема модели и результаты моделирования работы отделения банка при наличии двух операторов-кассиров

 

Блок SignalScope характеризует процедуру прохождения требований через накопитель. Из графика, изображенного на рисунке 3, видно, что не все заявки сразу поступают на обслуживание, некоторые заявки формируют очередь.

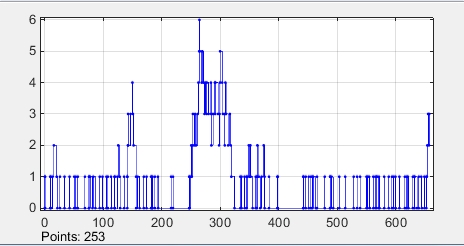
Рисунок 3. Процедура прохождения заявок через накопитель

По результатам проведения имитационного моделирования работы отделения банка по обслуживанию физических лиц можно сделать следующие выводы:

– в течение одного рабочего дня в отделение приходит в среднем 128 клиентов, из которых в течение рабочего дня обслуженными оказываются 123 клиента, т.е. относительная пропускная способность составляет 96.1%;

– среднее время ожидания клиентом обслуживания составляет 2.81 минуты;

– среднее число клиентов, находящихся в очереди составляет 0.54 человека;

– на момент закрытия в очереди остается 3 требования и двое клиентов находятся на обслуживании операторами;

– в течение рабочего дня оба оператора оказываются примерно одинаково загруженными, при этом первый оператор обслуживает 55.3% поступивших на обслуживание требований. Коэффициент использования системы составляет 60.6%.

Очевидно, что относительная пропускная способность данной системы достаточно высокая, среднее время пребывания клиентов в очереди весьма непродолжительное. Анализ других характеристик эффективности обслуживания при наличии двух операторов-кассиров свидетельствует об отсутствии перегрузки в работе данного отделения.

Выводы

Созданная имитационная модель системы массового обслуживания средствами табличного процессора MS Excel вполне адекватно отражает работу отделения банка и может быть применена для моделирования аналогичных систем массового обслуживания наравне со специализированными программными продуктами.

Созданная имитационная модель СМО отделения банка позволяет проводить оптимизацию наиболее значимых параметров системы и может быть составной частью системы поддержки принятия решений для рационализации организационной структуры и оптимизации управления.

Результаты работы модели можно считать корректными при достоверных исходных данных. Проведенный эксперимент показал, что затраты компьютерного времени, которые считаются одним из основных недостатков имитационного моделирования, не являются критичными при реальных параметрах СМО. Полученные результаты подтверждают эффективность методов компьютерного имитационного моделирования для диагностики и оптимизации систем массового обслуживания.

Библиографический список

1. Антонова Г.М., Цвиркун А.Д. Оптимизационно-имитационное моделирование для решения проблем оптимизации современных сложных производственных систем// Проблемы управления. 2005. – № 5. – С.19-27.
2. Бирюков А.Н. Имитационное моделирование как элемент управления рисками для укрепления финансового положения фирмы// Иннов: электронный научный журнал, 2016. №4 (29). URL: http://www.innov.ru/science/economy/imitatsionnoe-modelirovanie-kak-ele/
3. Бобков С.П., Иванников А.И., Урюпина Н.М. Оптимизация структуры системы массового обслуживания// Современные наукоемкие технологии. Региональное приложение. 2006. – № 3. – С. 3-5.
4. Бояршинова И.Н., Исмагилов Т.Р., Потапова И.А. Моделирование и оптимизация работы системы массового обслуживания// Фундаментальные исследования. – 2015. - № 9-1. – С. 9-13.
5. Буянов Б.Б., Лубков Н.В., Поляк Г.Л. Система поддержки принятия управленческих решений с применением имитационного моделирования// Проблемы управления. 2006. – № 6. – С.43-49.
6. Влацкая И.В., Татжибаева О.А. Применение методов имитационного моделирования в реинжиниринге бизнес процессов// Вестник ОГУ. 2010. –№ 9 (115). – С.98-103.
7. Галиуллина А.Ф., Сильнова С.В., Черняховская Л.Р. Оценка эффективности управления производственным процессом с применением имитационного моделирования на основе систем массового обслуживания// Вестник УГАТУ. 2015. – Т.19. № 1 (67). – С. 184-191.
8. Горемыкина Г.И., Пономарёва М.А. К вопросу о применении имитационного моделирования в управлении бизнес-процессами в условиях нестабильной экономической ситуации// Проблемы управления и моделирования в сложных системах: труды XI Межд. конф. – Самара, 2009. – С. 503-508.
9. Гультяев А.К. Визуальное моделирование в среде MATLAB. – СПб.: Питер, 2000. – 432 с.
10. Данилец Е.В., Райко Г.А., Игнатенко Г.А. Использование имитационного моделирования для анализа систем управления предприятием// Вестник Херсонского национального технического университета. 2011. – № 4 (43). – С. 157-161.
11. Дуплякин В.М., Княжева Ю.В. Выбор закона распределения входного потока заявок при моделировании системы массового обслуживания торгового предприятия// Вестн. Самарского гос. аэрокосмического ун-та им. академика С.П. Королёва (нац. исслед. ун-та). 2012. – № 6 (37). – С. 102-111.
12. Изюмский А.А., Надирян С.Л., Сенин И.С. Применение имитационного моделирования в сфере моделирования транспортных потоков// Наука. Техника. Технологии (политехнический вестник). 2016. – № 1. – С. 52-54.
13. Кельтон В., Лоу А. Имитационное моделирование. Классика CS. 3-е изд. – СПб.: Питер: Киев: Издательская группа BHV, 2004. – 847 с.
14. Княжева Ю.В. Повышение эффективности системы массового обслуживания торгового предприятия посредством численного статистического моделирования// Вест. Новосиб. гос. ун-та. Серия: Социально-экономические науки. 2014. – Т. 14, вып. 2. – С. 83-100.
15. Крупский А.Ю., Монахов А.Д. Инновации в имитационном моделировании// Интернет-журнал Науковедение. 2011. – №2 (7). – С. 28.
16. Курманаева Ф.Р., Китаева О.И., Курзаева Л.В. К вопросу об имитационном моделировании в системе Arena// Современная техника и технологии. 2016. – № 12-2 (64). – С. 91-93.
17. Макова А.С. Перспективы развития имитационного моделирования// Современные наукоемкие технологии. 2014. – № 7-1. – С. 59-60.
18. Полянская Я.В., Егорова Т.Д. Проектирование работы предприятия на основе имитационного моделирования// Вестник АГТУ. 2007. – № 4. – С. 84-86.
19. Романенко В.А. Векторная оптимизация параметров системы массового обслуживания с нестационарными потоками и частичной взаимопомощью между каналами// Вестн. Самарского гос. аэрокосмического ун-та им. академика С.П. Королёва (нац. исслед. ун-та). 2011. – № 6 (30). – С. 264-272.
20. Хмелевская А.В., Коптев Д.С., Шевцов А.Н., Щитов А.Н. Алгоритм имитационного моделирования системы массового обслуживания в среде динамического моделирования MATLAB/Simulink// Известия Юго-Западного государственного университета. Серия: Управление, вычислительная техника, информатика. Медицинское приборостроение. 2016. – № 1 (18). – С. 77-90.
21. Алетдинова А.А., Королева Н.С. Влияние информационно-коммуникационных технологий на тенденции постмодернистского строя жизни // ИТпортал, 2016. №4 (12). URL: http://itportal.ru/science/tech/vliyanie-informatsionno-kommunikats/
22. Кожухарь В.И., Кузьмичев И.К., Сергеева Т.С. Антикризисное управление // конспект лекций по дисциплине "Антикризисное управление" для студентов специальности 0611 "Менеджмент организации" / В. И. Кожухарь, И. К. Кузьмичев, Т. С. Сергеева ; М-во трансп. Рос. Федерации, Федер. гос. образоват. учреждение высш. проф. образования Волж. гос. акад. вод. трансп., Каф. упр. трансп.. Н. Новгород, 2004.
23. Якимов И.М., Кирпичников А.П., Мокшин В.В. Моделирование сложных систем в среде имитационного моделирования GPSS W с расширенным редактором// Вестник Казанского технологического университета. 2014. – Т. 17. № 4. – С. 298-303.


References

1. Antonova G. M., TSvirkun A. D. Optimizacionno-imitacionnoe modelirovanie dlja reshenija problem optimizacii sovremennyh slozhnyh proizvodstvennyh system. Problemy upravlenija. 2005. No 5. Pp.19-27.
2. Birjukov A.N. Imitacionnoe modelirovanie kak jelement upravlenija riskami dlja ukreplenija finansovogo polozhenija firmy. Innov: jelektronnyj nauchnyj zhurnal, 2016. №4 (29). URL: http://www.innov.ru/science/economy/imitatsionnoe-modelirovanie-kak-ele/
3. Bobkov S.P., Ivannikov A.I., Urjupina N.M. Optimizacija struktury sistemy massovogo obsluzhivanija. Sovremennye naukoemkie tehnologii. Regional'noe prilozhenie. 2006. No 3. Pp. 3-5.
4. Bojarshinova I.N., Ismagilov T.R., Potapova I.A. Modelirovanie i optimizacija raboty sistemy massovogo obsluzhivanija. Fundamental'nye issledovanija. 2015. No 9-1. Pp. 9-13.
5. Bujanov B. B., Lubkov N. V., Poljak G. L. Sistema podderzhki prinjatija upravlencheskih reshenij s primeneniem imitacionnogo modelirovanija. Problemy upravlenija. 2006. No 6. Pp.43-49.
6. Vlackaja I.V., Tatzhibaeva O.A. Primenenie metodov imitacionnogo modelirovanija v reinzhiniringe biznes processov. Vestnik OGU. 2010. No 9 (115). Pp. 98-103.
7. Galiullina A.F., Sil'nova S.V., Chernjahovskaja L.R. Ocenka jeffektivnosti upravlenija proizvodstvennym processom s primeneniem imitacionnogo modelirovanija na osnove sistem massovogo obsluzhivanija. Vestnik UGATU. 2015. T.19. No 1 (67). Pp. 184-191.
8. Goremykina G.I., Ponomarjova M.A. K voprosu o primenenii imitacionnogo modelirovanija v upravlenii biznes-processami v uslovijah nestabil'noj jekonomicheskoj situacii// Problemy upravlenija i modelirovanija v slozhnyh sistemah: trudy XI Mezhd. konf. – Samara, 2009. – S. 503-508.
9. Gul'tjaev A.K. Vizual'noe modelirovanie v srede MATLAB. SPb.: Piter, 2000. 432 p.
10. Danilec E.V., Rajko G.A., Ignatenko G.A. Ispol'zovanie imitacionnogo modelirovanija dlja analiza sistem upravlenija predprijatiem. Vestnik Hersonskogo nacional'nogo tehnicheskogo universiteta. 2011. No 4 (43). Pp. 157-161.
11. Dupljakin V.M., Knjazheva Ju.V. Vybor zakona raspredelenija vhodnogo potoka zajavok pri modelirovanii sistemy massovogo obsluzhivanija torgovogo predprijatija. Vestn. Samarskogo gos. ajerokosmicheskogo un-ta im. akademika S.P. Koroljova (nac. issled. un-ta). 2012. No 6 (37). Pp. 102-111.
12. Izjumskij A.A., Nadirjan S.L., Senin I.S. Primenenie imitacionnogo modelirovanija v sfere modelirovanija transportnyh potokov. Nauka. Tehnika. Tehnologii (politehnicheskij vestnik). 2016. No 1. Pp. 52-54.
13. Kel'ton V., Lou A. Imitacionnoe modelirovanie. Klassika CS. 3-e izd. SPb.: Piter: Kiev: Izdatel'skaja gruppa BHV, 2004. 847 p.
14. Knjazheva Ju.V. Povyshenie jeffektivnosti sistemy massovogo obsluzhivanija torgovogo predprijatija posredstvom chislennogo statisticheskogo modelirovanija. Vest. Novosib. gos. un-ta. Serija: Social'no-jekonomicheskie nauki. 2014. T. 14, vyp. 2. Pp. 83-100.
15. Krupskij A.Ju., Monahov A.D. Innovacii v imitacionnom modelirovanii. Internet-zhurnal Naukovedenie. 2011. No 2 (7). Pp. 28.
16. Kurmanaeva F.R., Kitaeva O.I., Kurzaeva L.V. K voprosu ob imitacionnom modelirovanii v sisteme Arena// Sovremennaja tehnika i tehnologii. 2016. № 12-2 (64). Pp. 91-93.
17. Makova A.S. Perspektivy razvitija imitacionnogo modelirovanija. Sovremennye naukoemkie tehnologii. 2014. No 7-1. Pp. 59-60.
18. Poljanskaja Ja.V., Egorova T.D. Proektirovanie raboty predprijatija na osnove imitacionnogo modelirovanija. Vestnik AGTU. 2007. No 4. Pp. 84-86.
19. Romanenko V.A. Vektornaja optimizacija parametrov sistemy massovogo obsluzhivanija s nestacionarnymi potokami i chastichnoj vzaimopomoshh'ju mezhdu kanalami. Vestn. Samarskogo gos. ajerokosmicheskogo un-ta im. akademika S.P. Koroljova (nac. issled. un-ta). 2011. No 6 (30). Pp. 264-272.
20. Hmelevskaja A.V., Koptev D.S., Shevcov A.N., Shhitov A.N. Algoritm imitacionnogo modelirovanija sistemy massovogo obsluzhivanija v srede dinamicheskogo modelirovanija MATLAB/Simulink. Izvestija Jugo-Zapadnogo gosudarstvennogo universiteta. Serija: Upravlenie, vychislitel'naja tehnika, informatika. Medicinskoe priborostroenie. 2016. No 1 (18). Pp. 77-90.
21. Aletdinova A.A., Koroleva N.S. Vlijanie informacionno-kommunikacionnyh tehnologij na tendencii postmodernistskogo stroja zhizni // ITportal, 2016. №4 (12). URL: http://itportal.ru/science/tech/vliyanie-informatsionno-kommunikats/
22. Kozhuhar' V.I., Kuz'michev I.K., Sergeeva T.S. Antikrizisnoe upravlenie konspekt lekcij po discipline "Antikrizisnoe upravlenie" dlja studentov special'nosti 0611 "Menedzhment organizacii" / V. I. Kozhuhar', I. K. Kuz'michev, T. S. Sergeeva ; M-vo transp. Ros. Federacii, Feder. gos. obrazovat. uchrezhdenie vyssh. prof. obrazovanija Volzh. gos. akad. vod. transp., Kaf. upr. transp.. N. Novgorod, 2004.
23. Jakimov I.M., Kirpichnikov A.P., Mokshin V.V. Modelirovanie slozhnyh sistem v srede imitacionnogo modelirovanija GPSS W s rasshirennym redaktorom. Vestnik Kazanskogo tehnologicheskogo universiteta. 2014. T. 17. No 4. Pp. 298-303.

Tweet

Яндекс.ВиджетINNOV