Аннотация: Статья посвящена вопросу нахождения постоянных и переменных возмущающих сил и моментов, возникающих в соединении роторов жёсткой муфтой при наличии расцентровки осей соединяемых валов. Выведенные зависимости позволяют определить перемещения концов соединяемых валов, а также деформации и напряжения, возникающие в валах под действием найденных возмущающих сил. Данная проблема является важной и актуальной, так как расцентровка жёстких соединительных муфт возникает всегда из-за неточностей их изготовления, сборки и смещений при работе. Расцентровка может оказать существенное влияние на напряжённо-деформированное состояние роторной системы, хотя в современных расчётах чаще всего не учитывается.

Приведён краткий обзор муфт, применяемых в роторных системах для соединения валов. Показаны виды несоосностей осей соединяемых валов (расцентровок). Поставлена цель настоящей работы - определение постоянных и переменных сил и моментов, возникающих в жёстких муфтах при расцентровках. Приведена расчётная схема движения концов расцентрованных роторов и выведены системы уравнений, решение которых позволяет рассчитать постоянные и переменные силы и моменты, действующие на концы валов. Описана методика, составленная на основе выведенных зависимостей, позволяющая использовать их для расчёта деформаций концов валов и возникающих в них напряжений. В конце статьи делаются выводы и даются рекомендации по использованию разработанной методики при проектировании вновь создаваемых и совершенствовании существующих роторных установок.

Annotation: Article is devoted to a question of finding of constant and variable perturbing forces and mo-ments arising in connection of rotors by rigid coupling in the presence of a misalignment of axes of the connected shafts. The derived dependences allow to define relocation of the ends of the connected shafts, and also the deformations and tension arising in shaft under the influence of the found perturbing forces. This problem is important and urgent as the misalignment of rigid connections arises always because of inaccuracies of their manufacture, assembly and offsets in operation. The misalignments can have significant effect on the intense deformed status of rotor system though in the modern calculations most often are not considering.

The short review of the couplings applied in rotor systems to connection of shaft is provided. Types of nonaxialities of the connected shafts (misalignments) are shown. The object of this investigation is the determination of the constant and variable forces and the moments arising in rigid couplings in case of it’s misalignments. The estimated diagram of movement of the ends of misalignmented rotors is provided and systems of equations which solution allows to calculate the constant and variable forces and the moments operating for the ends of shaft are derived. The technique made on the basis of the derived dependences, allowing to use them for calculation of deformations of the ends of shafts and tension arising in them is described. At the end of article conclusions are drawn and usage considerations of the developed technique in case of design of developing and enhancement of the existing rotor installations are given.

Введение 

При создании установок, имеющих в своём составе роторы, применяются соединительные муфты, использование которых не должно приводить к превышению нормативного уровня вибрации. На вибрацию оказывают сильное влияние конструктивные особенности и характеристики муфт, главная из которых – способность муфт компенсировать неизбежные расцентровки осей валов и снижать степень взаимовлияния валов в роторной системе.

По принципу работы конструкции муфт можно разделить на подвижные и жёсткие [1, 2, 3].

Подвижные соединительные муфты [4, 5] применяются для обеспечения относительных осевых смещений валов при их тепловых расширениях, в тех случаях, когда приводной механизм не допускает смещений ротора относительно статора и имеет в своём составе упорный подшипник, для компенсации расцентровок валов и для уменьшения взаимовлияния валов в роторных системах. Методы расчёта таких муфт рассматривались, например, в [6, 7, 8, 9]. Также в существующей на данный момент литературе предлагается множество путей совершенствования подвижных соединительных муфт [10, 11, 12].

Жёсткие муфты наиболее просты в изготовлении и компактны. В большинстве случаев они выполняются в виде двух хорошо пригнанных по плоскостям фланцев, скреплённых при помощи призонных болтов. Такая конструкция способна передавать высокий крутящий момент и применяется во многих тяжелонагруженных роторных машинах [13, 14].

Некоторые виды подвижных муфт (например, зубчатые или шлицевые) в условиях сильных расцентровок также могут вести себя как жёсткое соединение, и компенсация расцентровок осуществляется только за счёт деформации соединяемых валов.

При жёстком соединении валов роторная система превращается в статически неопределимый многоопорный валопровод, нагрузка на его опорные подшипники зависит от веса ротора от его жесткостных характеристик, податливости подшипниковых опор и фундаментных конструкций, а также от уровня их нагрева, тепловой стабильности и действующих на них сил [15, 20].

Постановка задачи 

Целью данной работы является разработка методики расчёта постоянных и переменных сил и моментов в соединении роторов жёсткой муфтой при расцентровке осей соединяемых валов, а также деформаций валов в месте расположения муфты.

Для оценки вибрационного и напряжённо-деформированного состояния роторной системы с жёстким соединением валов необходимо произвести расчёт уровней динамических сил, возникающих из-за несоосности соединяемых валов.

Поскольку расцентровка осей валов является кинематическим возбудителем колебаний роторов, то силы и моменты, возникающие в месте соединения роторов, зависят от степени сопротивления роторов деформированию, т.е. от инерционно-жесткостных характеристик валов, входящих в роторную систему, и их опор.

Расцентровка (несоосность) соединяемых муфтой валов может быть двух видов [16, 17]:

1) Радиальная (параллельное смещение концов валов);

2) Угловая (взаимный поворот концов валов в местах расположения полумуфт).

Вначале рассматривалось поведение валов при радиальной расцентровке.

В качестве исходных данных используются следующие величины:

- радиальная расцентровка соединяемых роторов Δ_y;

- геометрические размеры элементов роторов;

- модули упругости материалов роторов Е;

- массы элементов роторов.

Разработка методики 

Схема соединения валов с параллельно смещёнными в вертикальной плоскости осями показана на рис. 1.

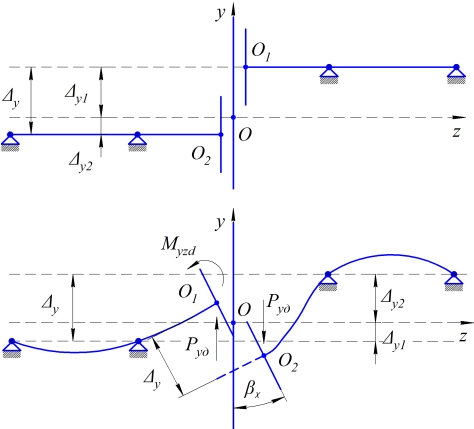
Рис. 1. Валы с параллельно смещёнными в вертикальной плоскости осями.

Характерным для этой схемы является:

- расстояние между центрами валов постоянно: ;

- фланцы полумуфт поворачиваются при расцентровке на одинаковый угол: 

- поскольку принято, что система валов изотропна, то при вращении валов их центры  и  двигаются по окружностям с центром в точке О.

Введём следующие обозначения:

 – постоянная сила, действующая в вертикальной плоскости ;

 – постоянный момент, действующий в вертикальной плоскости ;

 и  – переменные силы, действующие в вертикальной () и в горизонтальной ( ) плоскостях;

 и  – переменные моменты, действующие в вертикальной () и в горизонтальной () плоскостях.

На рис. 2 показана схема движения концов валов.

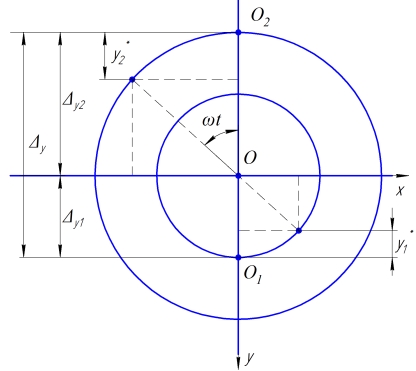
Рис. 2. Схема движения концов валов.

Для расчёта деформации ротора при расцентровках необходимо знать коэффициенты статической и динамической податливости соединяемых роторов при приложении к концу вала единичной силы и момента:

 - смещение конца вала от единичного вектора силы;

 - угол между направлением единичного вектора силы и смещением от него;

 - смещение конца вала от единичного момента;

 - угол между плоскостью действия единичного момента и смещением от него;

 - поворот плоскости полумуфты от единичного вектора силы;

 - угол между направлением поворота плоскости полумуфты и единичным вектором силы, вызывающим этот поворот;

 - поворот плоскости полумуфты от единичного момента;

 - угол между направлением поворота плоскости полумуфты и плоскостью действия единичного момента, вызывающего этот поворот.

Эти податливости должны вычисляться с учётом податливостей опор и свойств масляной плёнки в подшипниках. Их расчёт возможен с помощью точных формул сопромата (для простейших роторных систем), а также с помощью систем трёхмерного моделирования, использующих метод конечных элементов [18], например, Ansys, SolidWorks и др. На многих предприятиях имеются собственные программы [19].

Зная найденные коэффициенты, можно вычислить значения постоянных ( , ) и переменных (, ,  , ) сил и моментов с помощью системы (1) [20] – цифрой 1 в индексах обозначены коэффициенты для первого вала, цифрой 2 – коэффициенты для второго; индекс 0 имеют статические податливости, динамические податливости - без индекса:

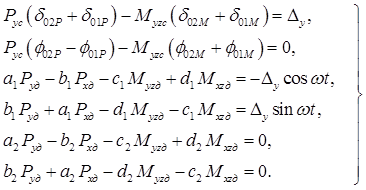                                               (1)

Формулы для расчёта коэффициентов а₁, b₁, c₁, d₁, а₂, b₂, c₂, d₂ приведены в системе (2) [20]:

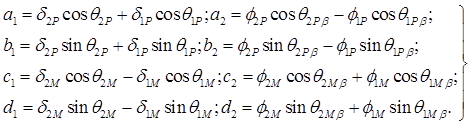  (2)

                          

Схема соединения валов с перекосом осей (поворотом полумуфт на угол   ) в вертикальной плоскости показана на рис. 3.

Характерным для этой схемы является:

- центры валов  и   совмещены;

- между фланцами муфты сохраняется постоянный угол .

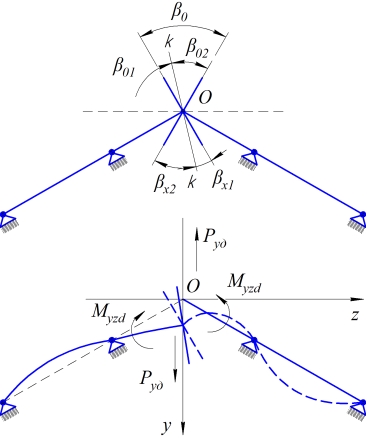
Рис. 3. Излом осей валов.

Поскольку принято, что система валов изотропна, то деформация валов при вращении будет такова, как если бы точки на поверхностях фланцев двигались по окружности относительно оси k–k (рис. 3), при этом поверхности фланцев будут описывать конические поверхности с вершиной в точке О.

Все обозначения остаются теми же, что и при параллельном смещении осей валов.

1. Определяются характеристики соединяемых роторов при приложении к концу вала единичной силы и момента (так же, как при радиальной расцентровке).

2. Вычисляем значения постоянных (  ,  ) и переменных (, ,  , ) сил и моментов с помощью системы (3) [21]:

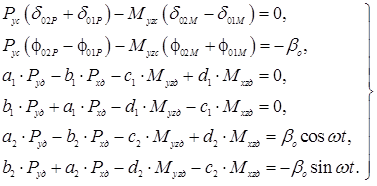                (3)                             

Формулы для расчёта коэффициентов а₁, b₁, c₁, d₁, а₂, b₂, c₂, d₂ приведены в системе уравнений (2).

Выводы и рекомендации 

Решение полученных уравнений позволяет найти следующие характеристики:

1) Если требуется определить не только амплитудные значения динамических сил и моментов , ,  и   при заданном значении , но и их фазовые соотношения, то решения следует находить в виде  и . Подставив эти зависимости в уравнения и сгруппировав выражения при  и , получим восемь уравнений для нахождения всех значений  и .

2) Если требуется определить только амплитудные значения , ,  и , то можно поступить проще.

При заданном значении  из полученных четырёх уравнений находятся промежуточные значения , ,  и   для выбранного значения   (например, для ). Поскольку центры валов совершают круговые движения, амплитудные значения сил и моментов будут равны

 и .

3) Задаваясь различными значениями , можно найти критическую скорость составного ротора.

4) Выведенные зависимости позволяют определить деформации валов и напряжения, возникающие в них под действием найденных возмущающих сил.

В связи с полученными результатами рекомендуется использование разработанной методики при проектировани роторных машин с жёсткими муфтами с целью учёта влияния расцентровки осей соединяемых валов на напряжённо-деформированное состояние роторов. Также данная методика будет полезна при исследовании существующих роторных машин для наиболее полного понимания причин возникновения повышенных напряжений и деформаций при их работе.

Библиографический список

1. Акладная Г. С. Судовые турбомашины: курс лекций. М.: Альтаир-МГАВТ. 2013. 64 с.
2. Фещенко В. Н. Справочник конструктора: учебно-практическое пособие. Кн. 1. Машины и механизмы. Москва-Вологда: Инфра-Инженерия. 2016. 400 с.
3. Испытание и расчет деталей машин: учебное пособие / В.Н. Бельков и др. Омск: Омский государственный технический университет, 2016. 160 c.
4. Каратаев О.Р. Основы проектирования: учебное пособие / Каратаев О.Р., Хамидуллина Д.А. Казань: Казанский национальный исследовательский технологический университет. 2016. 124 c.
5. Фролов Ю.М. Электрический привод: краткий курс: учебник для академического бакалавриата / Ю.М. Фролов, В.П. Шелякин; под ред. Ю.М. Фролова. М.: Юрайт. 2017. 253 с.
6. Ильичев В.Ю. Заричный А.Ф. Методика определения жёсткости резиновых элементов втулочно-пальцевых муфт. Проблемы современной науки и образования, М.: Олимп. 2016. 107 с.
7. Концевич В.Г., Алексенко О.В., Литвиненко Д.О. параметризация упругого элемента муфты турбокомпрессора низкого давления. Машиностроитель. 2016. № 6. С. 23-25.
8. Богачев В.Н., Аникина В.С. Расчет упругой муфты с резинометаллическими шарнирами. Справочник. Инженерный журнал с приложением. 2016. № 5 (230). С. 26-29.
9. Динамический анализ упругой муфты в составе судового валопровода. Цысс В.Г., Строков И.М., Сергаева М.Ю. Динамика систем, механизмов и машин. 2016. Т. 2. № 1. С. 54-61.
10. Упругие муфты с улучшенными компенсирующими свойствами. Паршукова Н.Ю., Коробейников К.А., Гончарова Н.А. Фундаментальные и прикладные исследования: проблемы и результаты. 2016. № 27. С. 116-121.
11. Турбина с совмещенными муфтами и подшипниками. Авруцкий Г.Д., Захаров А.Е., Лазарев М.В., Соболев А.С. Надежность и безопасность энергетики. 2015. № 3 (30). С. 37-40.
12. Принципы подбора материала для шарнирных сопряжений технологических и транспортных машин. Шестов А.Н., Фёдоров В.В., Прохоров В.Ю. Труды международного симпозиума Надежность и качество. 2016. № 2. С. 182-184.
13. Генерация и методы снижения виброакустической активности в газоперекачивающих агрегатах с газотурбинным приводом. Дроконов А.М., Дроконов А.Е. Вестник Брянского государственного технического университета. 2017. № 1 (54). С. 68-71.
14. Обоснование выбора профиля теплофикационной паротурбинной установки для реконструкции энергоблоков с турбинами Т-250/300-23.5. Валамин А.Е., Култышев А.Ю., Шибаев Т.Л., Гольдберг А.А., Сахнин Ю.А., Степанов М.Ю., Билан В.Н., Кадкина И.В. Теплоэнергетика. 2016. № 11. С. 14-20.
15. Силаев Г.В. Конструкция автомобилей и тракторов: учебник для вузов / Г.В. Силаев. М.: Юрайт. 2017. - 370 с.
16. Кунина П.С., Величко Е.И., Нижник А.Е., Музыкантова А.В., Абессоло М. Анализ дефектов опорных элементов газоперекачивающих агрегатов компрессорных станций магистральных газопроводов. Территория Нефтегаз. 2016. № 4. С. 68-75.
17. Исследование воздействия расцентровки валов турбокомпрессорной установки на ток статора приводного электродвигателя. Кипервассер М.В., Герасимук А.В. Наукоемкие технологии разработки и использования минеральных ресурсов. 2016. № 3. С. 346-349.
18. Сравнительный анализ методов технического диагностирования при оценке технического состояния объекта. Лепеш А.Г., Спроге Г.А. Технико-технологические проблемы сервиса. 2016. № 2 (36). С. 22-40.
19. Моделирование изгибной жесткости валов в зависимости от геометрических параметров и модуля упругости материала. Нгуен В.Х., Зайдес С.А. В сборнике: Жизненный цикл конструкционных материалов (от получения до утилизации). Материалы докладов V Всероссийской научно-технической конференции с международным участием. 2015. С. 344-350.
20. Татарских Б.Я., Федоров О.В. Организационно-технологические направления и резервы модернизации машиностроения Российской Федерации // Новые технологии. 2010. №6. С. 7.
21. Сидоров А.А., Полникова Т.В., Ямпольский И.Д, Ильичев В.Ю. Вибропрочность элементов турбомашин: Учебно-методическое пособие. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 200 с.


References

1. Akladnaya G. S. Sudovye turbomashiny: kurs lekcij. M.: Altair-MGAVT. 2013. 64 p.
2. Feshchenko V. N. Spravochnik konstruktora: uchebno-prakticheskoe posobie. Kn. 1. Mashiny i mekhanizmy. Moskva-Vologda: Infra-Inzheneriya. 2016. 400 p.
3. Ispytanie i raschet detalej mashin: uchebnoe posobie / V.N. Belkov i dr. Omsk: Omskij gosudarstvennyj tekhnicheskij universitet, 2016. 160 p.
4. Karataev O.R. Osnovy proektirovaniya: uchebnoe posobie / Karataev O.R., Hamidullina D.A. Kazan: Kazanskij nacionalnyj issledovatelskij tekhnologicheskij universitet. 2016. 124 p.
5. Frolov Y.M. Elektricheskij privod: kratkij kurs: uchebnik dlya akademicheskogo bakalavriata. Y.M. Frolov, V.P. SHelyakin; pod red. YU.M. Frolova. M.: Yurajt. 2017. 253 p.
6. Ilichev V.Y. Zarichnyj A.F. Metodika opredeleniya zhyostkosti rezinovyh ehle-mentov vtulochno-palcevyh muft. Problemy sovremennoj nauki i obrazovaniya, M.: Olimp. 2016. 107 p.
7. Koncevich V.G., Aleksenko O.V., Litvinenko D.O. Parametrizaciya uprugogo ehlementa mufty turbokompressora nizkogo davleniya. Mashinostroitel. 2016. No 6. Pp. 23-25.
8. Bogachev V.N., Anikina V.S. Raschet uprugoj mufty s rezinometallicheskimi sharnirami. Spravochnik. Inzhenernyj zhurnal s prilozheniem. 2016.No 5 (230). Pp. 26-29.
9. Dinamicheskij analiz uprugoj mufty v sostave sudovogo valoprovoda. Cyss V.G., Strokov I.M., Sergaeva M.YU. Dinamika sistem, mekhanizmov i mashin. 2016. T. 2. No 1. Pp. 54-61.
10. Uprugie mufty s uluchshennymi kompensiruyushchimi svojstvami. Parshukova N.YU., Korobejnikov K.A., Goncharova N.A. Fundamentalnye i prikladnye issledovaniya: problemy i rezultaty. 2016. No 27. Pp. 116-121.
11. Turbina s sovmeshchennymi muftami i podshipnikami. Avruckij G.D., Zaharov A.E., Lazarev M.V., Sobolev A.S. Nadezhnost i bezopasnost ehnergetiki. 2015. Pp. 3 (30). Pp. 37-40.
12. Principy podbora materiala dlya sharnirnyh sopryazhenij tekhnologicheskih i transportnyh mashin. SHestov A.N., Fyodorov V.V., Prohorov V.Y. Trudy mezhdunarodnogo simpoziuma Nadezhnost i kachestvo. 2016. No 2. Pp. 182-184.
13. Generaciya i metody snizheniya vibroakusticheskoj aktivnosti v gazoperekachivayushchih agregatah s gazoturbinnym privodom. Drokonov A.M., Drokonov A.E. Vestnik Bryanskogo gosudarstvennogo tekhnicheskogo universiteta. 2017. No 1 (54). Pp. 68-71.
14. Obosnovanie vybora profilya teplofikacionnoj paroturbinnoj ustanovki dlya rekonstrukcii ehnergoblokov s turbinami T-250 300-23.5. Valamin A.E., Kultyshev A.YU., Shibaev T.L., Goldberg A.A., Sahnin Y.A., Stepanov M.YU., Bilan V.N., Kadkina I.V. Teploehnergetika. 2016. No 11. Pp. 14-20.
15. Silaev G.V. Konstrukciya avtomobilej i traktorov: uchebnik dlya vuzov / G.V. Silaev. M.: Yurajt. 2017. - 370 p.
16. Kunina P.S., Velichko E.I., Nizhnik A.E., Muzykantova A.V., Abessolo M. Analiz defektov opornyh ehlementov gazoperekachivayushchih agregatov kompressornyh stancij magistralnyh gazoprovodov. Territoriya Neftegaz. 2016. No 4. Pp. 68-75.
17. Issledovanie vozdejstviya rascentrovki valov turbokompressornoj ustanovki na tok statora privodnogo ehlektrodvigatelya. Kipervasser M.V., Gerasimuk A.V. Naukoemkie tekhnologii razrabotki i ispolzovaniya mineralnyh resursov. 2016. No 3. Pp. 346-349.
18. Sravnitelnyj analiz metodov tekhnicheskogo diagnostirovaniya pri ocenke tekhnicheskogo sostoyaniya objekta. Lepesh A.G., Sproge G.A. Tekhniko-tekhnologicheskie problemy servisa. 2016. No 2 (36). Pp. 22-40.
19. Modelirovanie izgibnoj zhestkosti valov v zavisimosti ot geometricheskih parametrov i modulya uprugosti materiala. Nguen V.H., Zajdes S.A. V sbornike: Zhiznennyj cikl konstrukcionnyh materialov (ot polucheniya do utilizacii). Materialy dokladov v Vserossijskoj nauchno-tekhnicheskoj konferencii s mezhdunarodnym uchastiem. 2015. Pp. 344-350.
20. Tatarskih B.Ja., Fedorov O.V. Organizacionno-tehnologicheskie napravlenija i rezervy modernizacii mashinostroenija Rossijskoj Federacii.Novye tehnologii. 2010. №6. P. 7.
21. Sidorov A.A., Polnikova T.V., Yampolskij I.D, Ilichev V.Y. Vibroprochnost ehlementov turbomashin: Uchebno-metodicheskoe posobie. M.: Izd-vo MGTU im. N.E. Baumana, 2004. 200 p.

Tweet

Яндекс.ВиджетINNOV